5 Jun 2023
Rigid Body Motion
Robot Kinematics
Robot Kinematics

Keypoints
- Rigid body motion
- Translation
- Rotation
- Transformation
- Representation of rotation
- Manipulaor Kinematics
Rigid body motion
- Rigid body motion: a motion of a rigid body in which particles of the body move through the same distances along parallel lines
- Rigid body motion is a combination of translation and rotation
- A mapping $g: \mathbb{R}^3 \rightarrow \mathbb{R}^3$ is a rigid body motion if and only iff:
- length is preserved: $\lVert g(\vec{x}) - g(\vec{y}) \rVert = \lVert \vec{x} - \vec{y} \rVert$
- cross product/orientation is preserved: $g(\vec{x}) \times g(\vec{y}) = g(\vec{x} \times \vec{y})$ for all $\vec{x}, \vec{y} \in \mathbb{R}^3$
Translation
$g(\vec{x}) = \vec{x} + \vec{t}$ for some $\vec{t} \in \mathbb{R}^3$
Rotation
$g(\vec{x}) = R\vec{x}$ for some $R \in SO(3)$.
- SO(3) is special orthogonal group, i.e. SO(3) = ${R \in \mathbb{R}^{3 \times 3}, R^TR = I, det(R) = 1}$
- $\lVert R\vec{p} - R\vec{q} \rVert = \lVert R(\vec{p}-\vec{q}) \rVert = \sqrt{[R(\vec{p}-\vec{q})]^TR(\vec{p}-\vec{q})} = \sqrt{(\vec{p}-\vec{q})^TR^TR(\vec{p}-\vec{q})} = \sqrt{(\vec{p}-\vec{q})^T(\vec{p}-\vec{q})} = \lVert\vec{p}-\vec{q}\rVert$
- Rotation about the $x$-axis by $\theta$: $R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\theta) & -sin(\theta) \\ 0 & sin(\theta) & cos(\theta) \end{bmatrix}$
- Rotation about the $y$-axis by $\theta$: $R_y(\theta) = \begin{bmatrix} cos(\theta) & 0 & sin(\theta) \\ 0 & 1 & 0 \\ -sin(\theta) & 0 & cos(\theta) \end{bmatrix}$
- Rotation about the $z$-axis by $\theta$: $R_z(\theta) = \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}$
- Rotation multiplication is not commutative: $R_x(\theta)R_y(\phi) \neq R_y(\phi)R_x(\theta)$
- Rotation multiplication is associative: $R_x(\theta)(R_y(\phi)R_z(\psi)) = (R_x(\theta)R_y(\phi))R_z(\psi)$
- Multi frames rotation: $R_{on} = R_{o1}R_{12}…R_{n-1,n}$
Representation of rotation
- Roatation matrix: $R \in SO(3)$
- Degree of freedom: 3.
- $R$ has 9 elements, but $R^TR = I$ and $det(R) = 1$, i.e. \(R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix}\) \(\begin{equation*} Constraint = \begin{cases} \vec{r_1}^T\vec{r_2} = 0 \\ \vec{r_2}^T\vec{r_3} = 0 \\ \vec{r_3}^T\vec{r_1} = 0 \\ \vec{r_1}^T\vec{r_1} = 1 \\ \vec{r_2}^T\vec{r_2} = 1 \\ \vec{r_3}^T\vec{r_3} = 1 \end{cases} \end{equation*}\) 9 elements - 6 constraints = 3 degree of freedom. DOF = #independent parameters - #independent constraints
- Euler angles:
- ZXZ: $R_{zxz}(\alpha, \beta, \gamma) = R_z(\alpha)R_x(\beta)R_z(\gamma)$. Body frame approach.
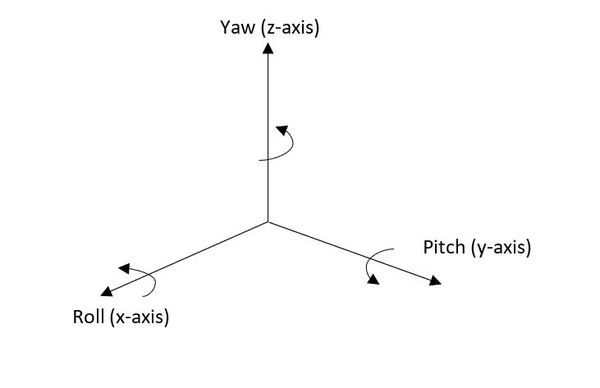
- Roll-Pitch-Yaw: $R_{rpy}(\alpha, \beta, \gamma) = R_z(\gamma)R_y(\beta)R_x(\alpha)$. Space/Fixed frame approach.
- Unit quaternions: $q = q_0 + q_1\hat{i} + q_2\hat{j} + q_3\hat{k} = (q_0, \vec{q})$, where $q_0$ is scalar part and $\vec{q}$ is vector part.
- $\hat{i}\hat{i}$ = $\hat{j}\hat{j}$ = $\hat{k}\hat{k}$ = -1, $\hat{i}\hat{j}$ = -$\hat{j}\hat{i}$ = $\hat{k}$, $\hat{j}\hat{k}$ = -$\hat{k}\hat{j}$= $\hat{i}$, $\hat{k}\hat{i}$ = -$\hat{i}\hat{k}$ = $\hat{j}$
- $q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1$
- Rotation about $\vec{w}$ by $\theta$:
- $q_0 = cos(\frac{\theta}{2})$
- $\vec{q} = sin(\frac{\theta}{2})\vec{w}$, where $\vec{w}$ is unit vector.
- $q^{-1} = (q_0, -\vec{q})$
- DOF = 4 - 1 = 3
- Exponential Coordinates for Rotation
- If $\vec{v} = \frac{d\vec{q}}{d\vec{t}} = \dot{\vec{q}} = \vec{w} \times \vec{q} = \hat{w}\vec{q}$ where $\vec{w}$ is angular velocity, so $\vec{q}(t) = e^{\hat{w}t}\vec{q}(0)$
- $\hat{w} = \begin{bmatrix} 0 & -w_3 & w_2 \\ w_3 & 0 & -w_1 \\ -w_2 & w_1 & 0 \end{bmatrix}$ and $\hat{w}^2 = \vec{w}\vec{w}^T - \lVert w \rVert I$
- $e^{\hat{w}t} = e^{\frac{\hat{w}}{\lVert \vec{w} \rVert}\lVert \vec{w} \rVert t} = e^{\hat{n}\theta}$ where $\lVert \vec{w} \rVert t=\theta, \vec{n} = \frac{\vec{w}}{\lVert \vec{w} \rVert}$, $\vec{n}$ is asix of rotation, $\theta$ is angle of rotation. Now let $\vec{n}$ be $\vec{w}$, so $e^{\hat{w}t} = e^{\hat{w}\theta}$. Left w is angular velocity, right w is axis of rotation.
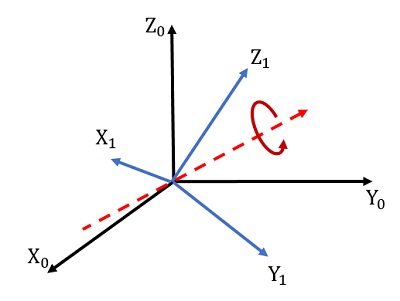
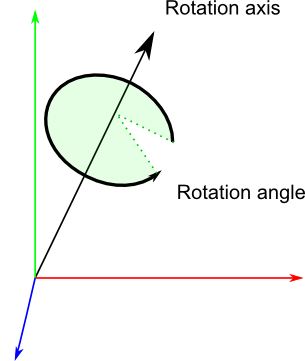
- $R(\vec{w}, \theta) = e^{\hat{w}\theta} = I + sin(\theta)\hat{w} + (1-cos(\theta))\hat{w}^2$ where $\lVert \vec{w} \rVert = 1$
- Exponentials of skew-symmetric matrices are rotation matrices. $e^{so(3)}=SO(3)$
- $(e^{\hat{w}\theta})^{-1} = (e^{\hat{w}\theta})^T = e^{\hat{w}(-\theta)}$, so $(e^{\hat{w}\theta})^T(e^{\hat{w}\theta}) = I$
- $det(e^{\hat{w}\theta}) = 1$
- Rodrigues’ formula: $e^{\hat{w}\theta} = I + sin(\theta)\hat{w} + (1-cos(\theta))\hat{w}^2$ where $\lVert \vec{w} \rVert = 1$. It’s to convert axis-angle representation to rotation matrix and convenient for computation/coding.
- Relationship among Roll-Pitch-Yaw & Rotation matrix & Axis/angle
- Euler to rotation matries: $R_{rpy}(\alpha, \beta, \gamma) = R_z(\gamma)R_y(\beta)R_x(\alpha)$
# (roll, pitch ,yaw)转换为3*3旋转矩阵
def euler2rotm(self, euler):
R_x = np.array([[1, 0, 0],
[0, np.cos(euler[0]), -np.sin(euler[0])],
[0, np.sin(euler[0]), np.cos(euler[0])]
])
R_y = np.array([[np.cos(euler[1]), 0, np.sin(euler[1])],
[0, 1, 0],
[-np.sin(euler[1]), 0, np.cos(euler[1])]
])
R_z = np.array([[np.cos(euler[2]), -np.sin(euler[2]), 0],
[np.sin(euler[2]), np.cos(euler[2]), 0],
[0, 0, 1]
])
R = np.dot(R_z, np.dot(R_y, R_x))
return R
- Rotation matrices to Euler: $[\alpha, \beta, \gamma]^T = [atan2(r_{32}, r_{33}), atan2(-r_{31}, \sqrt{r_{11}^2 + r_{21}^2}), atan2(r_{21}, r_{11})]^T$
# 旋转矩阵转换为欧拉角:roll, pitch, yaw
def rotm2euler(self, R):
sy = math.sqrt(R[0,0] * R[0,0] + R[1,0] * R[1,0])
singular = sy < 1e-6
if not singular :
x = math.atan2(R[2,1] , R[2,2])
y = math.atan2(-R[2,0], sy)
z = math.atan2(R[1,0], R[0,0])
else :
x = math.atan2(-R[1,2], R[1,1])
y = math.atan2(-R[2,0], sy)
z = 0
return np.array([x, y, z])
- Rotation matrices to Axis/angle: $\theta = acos(\frac{tr(R) - 1}{2})$, $w = \frac{1}{2sin(\theta)}(R-R^T) \check{}= \frac{1}{2sin(\theta)}[r_{32} - r_{23}, r_{13} - r_{31}, r_{21} - r_{12}]^T$
# 旋转矩阵转换为轴角表示
def rotm2axisangle(self, R):
theta = math.acos((np.trace(R) - 1) / 2)
w = 1 / (2 * math.sin(theta)) * np.array([R[2, 1] - R[1, 2], R[0, 2] - R[2, 0], R[1, 0] - R[0, 1]])
return w, theta
- Axis/angle to rotation matries: Rodrigues’ formula $e^{\hat{w}\theta} = I + sin(\theta)\hat{w} + (1-cos(\theta))\hat{w}^2$
# 轴角表示转换为旋转矩阵
def axisangle2rotm(self, w, theta):
w = w / np.linalg.norm(w)
wx, wy, wz = w[0], w[1], w[2]
w_hat = np.array([[0, -wz, wy],
[wz, 0, -wx],
[-wy, wx, 0]])
R = np.eye(3) + np.sin(theta) * w_hat + (1 - np.cos(theta)) * np.dot(w_hat, w_hat)
return R
$g(\vec{x}) = R\vec{x} + \vec{p}$ for some $R \in SO(3)$ and $\vec{p} \in \mathbb{R}^3$
- First translate, then rotate. Otherwise, the translation will be rotated as well.
- $\vec{v_b} = R_{ab}\vec{v_b}$, where $R_{ab}$ is the rotation matrix from frame $a$ to frame $b$
- $\vec{p_b} = \vec{p_a} + \vec{p_{ab}}$, where $\vec{p_{ab}}$ is the position vector of frame $b$ in frame $a$
- Special Euclidean Group: SE(3) = ${(\vec{p}, R), \vec{p} \in \mathbb{R}^3, R \in SO(3)}$
- $g_1(g_2(\vec(q))) = g_1(\vec{p_2} + R_2\vec{q}) = \vec{p_1} + R_1(\vec{p_2} + R_2\vec{q}) = (\vec{p_1} + R_1\vec{p_2}) + (R_1R_2)\vec{q} = g_1g_2(\vec{q})$, so $g_1 \circ g_2 = (\vec{p_1} + R_1\vec{p_2}, R_1R_2)$
- $g^{-1}(\vec{q}) = g^{-1}(\vec{p} + R\vec{q}) = R^T(\vec{q} - \vec{p}) = (R^T\vec{q} - R^T\vec{p}, R^T)$, so $g^{-1} = (-R^T\vec{p}, R^T)$
Manipulator Kinematics
Homogeneous Coordinates
- $\vec{p} = (x, y, z)^T \rightarrow \vec{p} = (x, y, z, 1)^T$
- $\vec{v} = \vec{p} - \vec{q} = (x, y, z, 1)^T - (x’, y’, z’, 1)^T = (x - x’, y - y’, z - z’, 0)^T$
- $g(\vec{q}) = R\vec{q} + \vec{p} = \begin{bmatrix} R & \vec{p} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \vec{q} \\ 1 \end{bmatrix}$, where $\begin{bmatrix} R & \vec{p} \\ 0 & 1 \end{bmatrix}$ is the homogeneous transformation matrix of $g \in SE(3)$
- Too complicated to write here (including figure), refers to RDKDC notes page 74 blue-line box.
- The se(3) = $\begin{bmatrix} \hat{\omega} & \vec{v} \\ 0 & 0 \end{bmatrix}$ $\hat{\omega} \in so(3)$, $\vec{v} \in \mathbb{R}^3$ is the Lie algebra of SE(3), where $\hat{w}$ is the axis of rotation, $\vec{v} = -\vec{w} \times \vec{q}$.
- Define $\hat{\xi} = \begin{bmatrix} \hat{\omega} & \vec{v} \\ 0 & 0 \end{bmatrix} \in \mathbb{R^{4\times4}}$ as
twist. $\vec{\xi} = (\vec{v}, \vec{\omega})^T \in \mathbb{R}^6$ is twist coordinates of $\hat{\xi}$. - If $\vec{w}=\vec{0}$, then $\hat{\xi} = \begin{bmatrix} 0 & \vec{v} \\ 0 & 0 \end{bmatrix}$, then $e^{\hat{\xi}} = \begin{bmatrix} I & \vec{v}\theta \\ 0 & 1 \end{bmatrix}$, which is a pure translation.
- If $\vec{w} \neq \vec{0}$, assume $\lVert \vec{w} \rVert = 1$, then $e^{\hat{\xi}} = \begin{bmatrix} R & \vec{p} \\ 0 & 1 \end{bmatrix}$, where $R = e^{\hat{\omega}\theta}$ and $\vec{p} = (I - e^{\hat{\omega}\theta})\vec{w} \times \vec{v} + \vec{w}\vec{w}^T\vec{v}\theta$
- $\hat{\xi’}$ w.r.t. body frame B, $\vec{\xi}$ w.r.t. space frame S. Then $\hat{\xi} = g_{ab}(0)\hat{\xi’}g_{ab}(0)^{-1}$, where $g_{ab}(0)$ is the homogeneous transformation matrix of frame B w.r.t. frame S at $\theta = 0$.
- All rigid transformation can be written as $e^{\hat{\xi}\theta}$.
- Example 2.2 on RDKDC page 82.
Forward Kinematics:
- Homogeneous representation of multi-joint manipulator: $g_{st}(\theta) = e^{\hat{\xi_1}\theta_1}e^{\hat{\xi_2}\theta_2}…e^{\hat{\xi_n}\theta_n}g_{st}(0)$, where $\xi_i$ is the twist of joint $i$ and $\theta_i$ is the joint angle of joint $i$